Su dominio esta definido por dos parámetros x y a que vienen a establecerse como sus valores mínimos y máximos que a menudo se denota como U(a,b)
La función de densidad viene dada de la forma

Donde:
a = Valor mínimo
b = Valor máximo
b – a = Rango
La función de distribución viene a ser
Esperanza
La media, valor medio esperado o esperanza matemática de una distribución uniforme se calcula empleando la siguiente fórmula:

Varianza

La probabilidad de que una observación caiga entre dos valores se calcula de la siguiente manera:
Su grafica viene expresada de esta forma
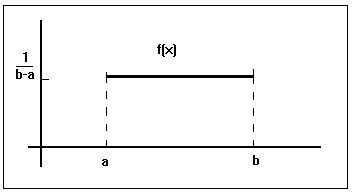
Ejercicio de Ejemplo
Suponga un experimento en el que de alguna manera se hace medición al azar y esta tiene una distribución uniforme en el intervalo [0,3]. Calcule la probabilidad de que la medición
este entre 1.5 y 2.
a) Por medio de su función de densidad.
b)Por medio de su función acumulada.
Solución A
a) Sea x la variable aleatoria continua definida en el experimento, se ha mencionado en las condiciones del problema que x tiene una distribución en [0,3]. Por lo tanto, su función de densidad estará dada por:
Tal que la probabilidad es:
Solución B
En esta ocasión X estará dada por:
Video explicativo:
Brian Rodriguez






La distribución uniforme es la símil de la distribución equiprobable de variable aleatoria discreta, y establece que en cualquier posición, dentro del rango de valores de la variable, la probabilidad de un suceso está en relación con la longitud del intervalo que lo define.
ResponderEliminarLa distribución uniforme es útil para describir una variable aleatoria con probabilidad constante sobre el intervalo(a,b)en el que está definida y se denota por U(a,b). También es conocida con el nombre de distribución rectangular por el aspecto de su función de densidad.
Una peculiaridad importante de esta distribución es que la probabilidad de un suceso depende exclusivamente de la amplitud del intervalo considerado y no de su posición en el campo de variación de la variable.
La distribución Uniforme es el modelo (absolutamente) continuo más simple. Corresponde al caso de una variable aleatoria que sólo puede tomar valores comprendidos entre dos extremos a y b, de manera que todos los intervalos de una misma longitud (dentro de (a, b)) tienen la misma probabilidad. También puede expresarse como el modelo probabilístico correspondiente a tomar un número al azar dentro de un intervalo (a, b).
ResponderEliminarEn teoría de probabilidad y estadística, la distribución uniforme continua es una familia de distribuciones de probabilidad para variables aleatorias continuas, tales que para cada miembro de la familia, todos los intervalos de igual longitud en la distribución en su rango son igualmente probables.
ResponderEliminar