lunes, 18 de mayo de 2020

Cuadro comparativo de variable aleatoria continua



por: Brian Rodriguez
en No hay comentarios:

Distribución chi cuadrado (χ2) de Pearson

La distribución chi cuadrado (χ2) de Pearson está íntimamente relacionada con la distribución normal.

Sean X con distribución X1, X2,..., Xn un conjunto de n variables aleatorias independientes con una distribución N (0,1), entonces una nueva variable aleatoria X = X21 + X22 +... + X2n sigue una distribución χ2n (chi cuadrado con n grados de libertad) y se representa así: X → χ2n. Su media y varianza valdrán μ = n y, σ2 = 2n. 

Esta distribución se usa para contrastar si la distribución de una variable se ajusta a una distribución determinada. 

Entre sus propiedades señalamos:

·              Nunca adopta valores menores de 0.

·              Es asimétrica positiva pero a medida que aumentan sus grados de libertad se va aproximando a la distribución normal.

·              Para n > 100 la podemos aproximar a una distribución N(n, √2n).

 

Su función de densidad es:


Donde  es la función gamma.

Formula x^2 es 


la varianza es:

2k

La esperanza es:

E(x)=k

Donde E(x) es la esperanza matemática de la variable aleatoria “x”

 

 


en 1 comentario:

Distribución normal

Distribución Normal

Se trata, sin duda, del modelo continuo más importante en estadística, tanto por su aplicación
directa, veremos que muchas variables de interés general pueden describirse por dicho modelo,
como por sus propiedades, que han permitido el desarrollo de numerosas técnicas de inferencia
estadística. En realidad, el nombre de Normal proviene del hecho de que durante un tiempo se
creyó, por parte de médicos y biólogos, que todas las variables naturales de interés seguían este
modelo.
¿Qué necesitamos para representar una distribución normal?
  •  Una variable aleatoria continúa.
  •  Calcular la media.
  •  Calcular la desviación típica.
  •  Decidir la función que queremos representar: función de densidad de probabilidad o función de distribución.
Ejemplo teórico

  •  Suponemos que queremos saber si los resultados de un examen pueden aproximarse satisfactoriamente a una distribución normal.
  •  Sabemos que en este examen participan 476 estudiantes y que los resultados podrán oscilar entre 0 y 10. Calculamos la media y la desviación típica a partir de las observaciones (resultados del examen).
  •  Entonces, definimos la variable aleatoria X como los resultados del examen que depende de cada resultado individual. Matemáticamente,
  •  La variable aleatoria X representa la variable resultados del examen y puede aproximarse a una distribución normal de media 4,8 y desviación típica de 3,09.
  •  El resultado de cada estudiante se anota en una tabla. De esta forma, obtendremos una visión global de los resultados y de su frecuencia.
Resultados Frecuencia
0-1-2-3-4-5-6-7-8-9-10 20-31-44-56-64-66-62-51-39-26-16
TOTAL 476

  •  Una vez hecha la tabla, representamos los resultados del examen y las frecuencias. Si el gráfico se parece a la imagen anterior y cumple con las propiedades, entonces, la variable resultados del examen puede aproximarse satisfactoriamente a una distribución normal de media 4,8 y desviación típica de 3,09. 

Histograma de frecuencias sobre la variable resultados del examen.

Su esperanza es: μ
Su varianza es: σ


por: Ricardo Melendez
Video: Brian Rodriguez
en 3 comentarios:

Distribución Gamma

La distribución Gamma está definida como los parámetros positivos  >0 y >0 para modelar valores de datos positivos que sean asimétricos a la derecha y mayores que 0. La distribución gamma se utiliza comúnmente en estudios de supervivencia de fiabilidad. 

Por ejemplo, la distribución gamma puede describir el tiempo que transcurre para que falle un componente eléctrico. La mayoría de los componentes eléctricos de un tipo particular fallará aproximadamente en el mismo momento, pero unos pocos tardarán más en fallar.

Su formula de densidad es



     {\displaystyle f(x)=\lambda e^{-\lambda x}{\frac {(\lambda x)^{k-1}}{\Gamma (k)}}}

Aquí  es el número e y  es la función gamma. Para valores  la función gamma es  (el factorial de ). En este caso - por ejemplo para describir un proceso de Poisson - se llaman la distribución Erlang con un parámetro .


Tal que: 



Esperanza 

{\displaystyle E[X]=k/\lambda =k\theta }


Varianza

{\displaystyle V[X]=k/\lambda ^{2}=k\theta ^{2}}

Ejercicio de ejemplo 

En una ciudad se observa que el consumo diario de energía (en millones de kilowatt-hora) es una variable aleatoria que sigue una distribución gamma con parámetros α= 3 y B=2. Si la planta de energía que suministra a la ciudad tiene una capacidad diaria de generar un máximo de 12, ¿cuál es la probabilidad de que haya un día donde no se pueda satisfacer la demanda?

Declaramos que 

donde, 
de la forma, 
     
La probabilidad de exista 1 exceso,

   
Resolviendo entonces, 
   

Video explicativo: 


Por: Ronney Matloo
Video: Barbara Delgado



en 3 comentarios:

Distribución Exponencial

La distribución exponencial se define como una distribución de probabilidad aleatoria usada en teoría de probabilidad la cual consta del parámetro el cual expresa que \lambda >0 y suele usarse para variables que describen el tiempo hasta que el dicho suceso ocurre. 

Su formula de densidad es la siguiente

{\displaystyle f(x)=\left\{{\begin{matrix}\lambda e^{-\lambda x}&\quad {\text{para }}x\geq 0\\0&\quad {\text{en caso contrario}}\end{matrix}}\right.}


Formula de distribución es

{\displaystyle F(x)=P(X\leq x)=\left\{{\begin{matrix}0&{\text{para }}x<0\\1-e^{-\lambda x}&{\text{para }}x\geq 0\end{matrix}}\right.}

Esperanza

Varianza 

Representado gráficamente como 


Ejercicio de ejemplo

El tiempo que transcurre antes de que una persona sea atendida en una cafetería es una variable aleatoria que tiene una distribución exponencial con una media de 4 minutos. ¿Cuál es la probabilidad de que una persona sea atendida antes de que transcurran 3 minutos en al menos 4 de los 6 días siguientes?

Declaramos entonces nuestra formula 


Donde  

x = número de días en que un cliente es atendido antes de que transcurran 3 minutos

x = 0, 1, 2,...,6 días

 


p = probabilidad de que un cliente sea atendido antes de que transcurran 3 minutos

 en un día cualquiera = 0.5276

q = probabilidad de que un cliente no sea atendido antes de que transcurran  3 minutos 

en un día cualquiera = 1- p = 0.4724


 

 

= 0.11587 + 0.02157 = 0.13744


https://www.youtube.com/watch?v=-MIj8qahdvw


por: Barbara Delgado

Video: Ricardo Melendez






en 3 comentarios:

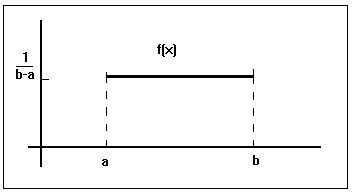
Distribución uniforme

Una variable uniforme es un conjunto de distribuciones de probabilidad usada para variables aleatorias continuas, tales para cada elemento perteneciente a ese conjunto de distribuciones todos los intervalos presentes son iguales para todas las distribuciones del conjunto tanto en su rango como longitud tales que, que dichos sucesos son igualmente probables en los parámetros establecidos. 

Su dominio esta definido por dos parámetros x y a que vienen a establecerse como sus valores mínimos y máximos que a menudo se denota como U(a,b) 
 

La función de densidad viene dada de la forma 

Monografias.com

Donde:

a = Valor mínimo

b = Valor máximo

b – a = Rango 

La distribución Uniforme


La función de distribución viene a ser 

F(x)=\left\{\begin{matrix} 0 & \mbox{para }x < a \\ \\ \frac{x-a}{b-a} & \ \ \ \mbox{para }a \le x < b \\ \\ 1 & \mbox{para }x \ge b \end{matrix}\right. \,\!

Esperanza 

La media, valor medio esperado o esperanza matemática de una distribución uniforme se calcula empleando la siguiente fórmula:

Monografias.com


Varianza

Monografias.com

La probabilidad de que una observación caiga entre dos valores se calcula de la siguiente manera:Monografias.com


Su grafica viene expresada de esta forma 
La Era de la Bioestadística" : Modelos de Probabilidad Continuos


Ejercicio de Ejemplo

Suponga un experimento en el que de alguna manera se hace medición  al azar y esta tiene una distribución uniforme en el intervalo [0,3]. Calcule la probabilidad de que la medición
este entre 1.5 y 2.

a) Por medio de su función de densidad.
b)Por medio de su función acumulada.

Solución A

a) Sea x  la variable aleatoria continua definida en el experimento, se ha mencionado en las condiciones del problema que x tiene una distribución en [0,3]. Por lo tanto, su función de densidad estará dada por:


Tal que la probabilidad es: 

Solución B

En esta ocasión X estará dada por:


Entonces tenemos que  es: 


Video explicativo: 

Brian Rodriguez




en 3 comentarios:

¿Qué es una variable aleatoria continua?

 Podemos definir una variable aleatoria continua como cualquier variable X que es continua si el conjunto de elementos o de posibles valores finitos o infinitos son números reales. 

En la práctica, se corresponden con variables asociadas con experimentos en los cuales la variable medida puede tomar cualquier valor en un intervalo: mediciones biométricas, intervalos de tiempo, áreas, etc.

Esta se divide en 2 partes las cuales constan de identificar una función de distribución acumulada y una función de densidad de probabilidad. También se debe distinguir entre una función de distribución acumulada y una función de densidad puesto que ambas tienes sus características. Esto aplicado con el fin de aplicar de una forma practica la relación entre la función de la densidad y la función de la distribución acumulada.  


Formulas de Variable continua, y densidad

Variable aleatoria 

      F(x) = P(X ≤ x)

Función de variable aleatoria continua

Esperanza

Si una X v.a.c el valor esperado o esperanza matemática de esa misma variable X, se puede denotar como E(x) o por el símbolo matemático μ

Varianza

  Varianza de una variabe aleatoria

Ronney Matloo

en No hay comentarios:
Suscribirse a: Entradas (Atom)