Distribución de variables aleatorias continuas
lunes, 18 de mayo de 2020
Distribución chi cuadrado (χ2) de Pearson
La distribución chi cuadrado (χ2) de Pearson está íntimamente relacionada con la distribución normal.
Sean X con distribución X1, X2,..., Xn un conjunto de n variables aleatorias independientes con una distribución N (0,1), entonces una nueva variable aleatoria X = X21 + X22 +... + X2n sigue una distribución χ2n (chi cuadrado con n grados de libertad) y se representa así: X → χ2n. Su media y varianza valdrán μ = n y, σ2 = 2n.
Esta distribución se usa para
contrastar si la distribución de una variable se ajusta a una distribución
determinada.
Entre sus propiedades señalamos:
·
Nunca adopta valores menores de 0.
·
Es asimétrica positiva pero a medida que aumentan sus grados de libertad
se va aproximando a la distribución normal.
·
Para n > 100 la podemos aproximar a una distribución N(n, √2n).
Su función de densidad es:
Donde
Formula x^2 es
la varianza es:
2k
La esperanza es:
E(x)=k
Donde E(x) es la
esperanza matemática de la variable aleatoria “x”
Distribución normal
- Una variable aleatoria continúa.
- Calcular la media.
- Calcular la desviación típica.
- Decidir la función que queremos representar: función de densidad de probabilidad o función de distribución.
- Suponemos que queremos saber si los resultados de un examen pueden aproximarse satisfactoriamente a una distribución normal.
- Sabemos que en este examen participan 476 estudiantes y que los resultados podrán oscilar entre 0 y 10. Calculamos la media y la desviación típica a partir de las observaciones (resultados del examen).
- Entonces, definimos la variable aleatoria X como los resultados del examen que depende de cada resultado individual. Matemáticamente,
- La variable aleatoria X representa la variable resultados del examen y puede aproximarse a una distribución normal de media 4,8 y desviación típica de 3,09.
- El resultado de cada estudiante se anota en una tabla. De esta forma, obtendremos una visión global de los resultados y de su frecuencia.
- Una vez hecha la tabla, representamos los resultados del examen y las frecuencias. Si el gráfico se parece a la imagen anterior y cumple con las propiedades, entonces, la variable resultados del examen puede aproximarse satisfactoriamente a una distribución normal de media 4,8 y desviación típica de 3,09.

Video: Brian Rodriguez
Distribución Gamma
 >0 y
>0 y  >0 para modelar valores de datos positivos que sean asimétricos a la derecha y mayores que 0. La distribución gamma se utiliza comúnmente en estudios de supervivencia de fiabilidad.
>0 para modelar valores de datos positivos que sean asimétricos a la derecha y mayores que 0. La distribución gamma se utiliza comúnmente en estudios de supervivencia de fiabilidad. 
 es el número e y
es el número e y  es la función gamma. Para valores
es la función gamma. Para valores  la función gamma es
la función gamma es  (el factorial de
(el factorial de  ). En este caso - por ejemplo para describir un proceso de Poisson - se llaman la distribución Erlang con un parámetro
). En este caso - por ejemplo para describir un proceso de Poisson - se llaman la distribución Erlang con un parámetro  .
.![{\displaystyle E[X]=k/\lambda =k\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/03d340b17d5f9a7627ca674a9e18b583f1da4b51)
![{\displaystyle V[X]=k/\lambda ^{2}=k\theta ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e10bb9a8029be7088506eee14cd33e4c0ad6d2c)
Video: Barbara Delgado
Distribución Exponencial
 y suele usarse para variables que describen el tiempo hasta que el dicho suceso ocurre.
y suele usarse para variables que describen el tiempo hasta que el dicho suceso ocurre. 

x = 0, 1, 2,...,6 días
p = probabilidad de que un cliente sea atendido antes de que transcurran 3 minutos
en un día cualquiera = 0.5276
q = probabilidad de que un cliente no sea atendido antes de que transcurran 3 minutos
en un día cualquiera = 1- p = 0.4724
= 0.11587 + 0.02157 = 0.13744
https://www.youtube.com/watch?v=-MIj8qahdvw
por: Barbara Delgado
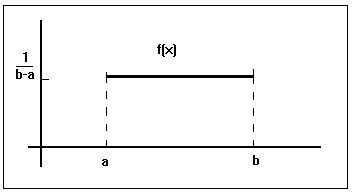
Distribución uniforme
La función de densidad viene dada de la forma

Donde:
a = Valor mínimo
b = Valor máximo
b – a = Rango
La función de distribución viene a ser
Esperanza
La media, valor medio esperado o esperanza matemática de una distribución uniforme se calcula empleando la siguiente fórmula:

Varianza

La probabilidad de que una observación caiga entre dos valores se calcula de la siguiente manera:
Ejercicio de Ejemplo
¿Qué es una variable aleatoria continua?
Formulas de Variable continua, y densidad
Variable aleatoria
F(x) = P(X ≤ x)
Función de variable aleatoria continua
Esperanza
Varianza




















